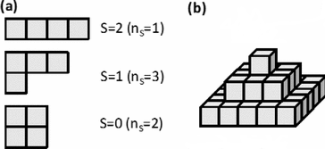
Irreducible representations of the SU(4) group for efficient simulations of open quantum systems with both collective and single-particle decoherence. This produces a pyramid structure of states that are SU(4) symmetric which allows the density matrix of an open cavity QED system to be block diagonal, drastically reducing the complexity of exact quantum simulations to polynomial scaling.
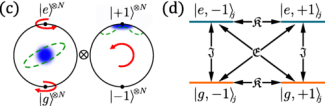
Three-axis twisting in a closed SU(4) system. The cavity interaction not only causes interparticle entanglement in both the spin degree of freedom and momentum degree of freedom, but also entangles the spin and momentum degrees of freedom with one another. Here, the system's dynamics are restricted to two internal states and two momentum states, which can be justified with a Kapitza-Dirac cavity.
Unlike the simple linear scaling of a system of particles in classical mechanics, a system of particles in quantum mechanics scales exponentially which makes direct simulation of anything but the smallest particle numbers impossible. This problem is compounded when considering open quantum systems, as these models are typically described in Liouville space which is a higher dimensional space whose elements are superoperators that act on both sides of a density matrix in order to encapsulate correlations with the environment. However, the symmetric coupling of atoms in cavity QED systems allowed our group to develop a groundbreaking exact quantum simulation of systems with both collective and single-particle decoherence whose numerical complexity is only polynomial-scaled with particle number. This simulation uses the irreducible representations of the SU(4) Lie group to find a permutationally symmetric subspace that forms a pyramid structure, and this pyramid is then used to rewrite the density matrix in a basis in which it is block diagonal with all other elements being zero and decoupled. Our work has been implemented in the Quantum Toolbox in Python (QuTiP) package by researchers from other universities.


 The Physics Frontiers Centers (PFC) program supports university-based centers and institutes where the collective efforts of a larger group of individuals can enable transformational advances in the most promising research areas. The program is designed to foster major breakthroughs at the intellectual frontiers of physics by providing needed resources such as combinations of talents, skills, disciplines, and/or specialized infrastructure, not usually available to individual investigators or small groups, in an environment in which the collective efforts of the larger group can be shown to be seminal to promoting significant progress in the science and the education of students. PFCs also include creative, substantive activities aimed at enhancing education, broadening participation of traditionally underrepresented groups, and outreach to the scientific community and general public.
The Physics Frontiers Centers (PFC) program supports university-based centers and institutes where the collective efforts of a larger group of individuals can enable transformational advances in the most promising research areas. The program is designed to foster major breakthroughs at the intellectual frontiers of physics by providing needed resources such as combinations of talents, skills, disciplines, and/or specialized infrastructure, not usually available to individual investigators or small groups, in an environment in which the collective efforts of the larger group can be shown to be seminal to promoting significant progress in the science and the education of students. PFCs also include creative, substantive activities aimed at enhancing education, broadening participation of traditionally underrepresented groups, and outreach to the scientific community and general public.